Beobachtungen:
Geschwindigkeit, Ausbreitungsgeschwindigkeit bei Wellen
Für Gegenstände oder auch für Wellen gibt es den Begriff Geschwindigkeit, und zwar ist dies das Verhältnis von zurückgelegtem Weg und dafür verbrauchter Zeit. Geschwindigkeit = Weg/Zeit
Beim Sport mißt man mit einer Stopuhr, bei höheren Ansprüchen mit Lichtschranken oder Zielfotos.
Auch aus einer akustischen Aufzeichnung mit Hilfe von Mikrofonen lassen sich Zeiten bestimmen.
Dieser Versuch mit einem fliegenden Sektkorken demonstriert die Anwendung der obigen Definition.
Bei Wellen unterscheidet man zwischen zwei Geschwindigkeiten:
Gruppengeschwindigkeit und Phasengeschwindigkeit.
Für die Bestimmung der Gruppengeschwindigkeit mißt man die Zeit, die beispielsweise zwischen dem Auftreffen eines Steines auf eine Wasseroberfläche und dem Ankommen der Wellengruppen am Ufer vergeht.
Bei der Phasengeschwindigkeit gilt die Zeit, die ein Wellensurfer für eine bestimmte Strecke benötigt, wenn er immer auf der abfallenden Flanke einer Welle, also bei gleicher Phase, sich befindet.
Beim Schall in Luft ist die Gruppengeschwindigkeit 340 m/s (abhängig von Wetterparametern: Temperatur, Luftfeuchte).
Bei Licht sind im Vakuum Phasen- und Gruppengeschwindigkeit gleich = 300 000 km/s.
Beispiel: Bestimmung der Geschwindigkeit eines Sektkorkens mit Hilfe der Schalls. Die Zeit zwischen Start und Ziel wird aus den Signalen zweier Mikrofone ermittelt. Gleichzeitig kommt bei dieser Messung auch die Größe der Schallgeschwindigkeit heraus.
Zusätzlich wird mit einer Hochgeschwindigkeitskamera der Anfang der Flugbahn aufgenommen. Dort hat der Korken die größte Geschwindigkeit. Im weiteren Flug wird er langsamer.
 |
| Abb. 01: Ein Sektkorken steckt
in einem Flaschenhals, daneben ein Mikrofon (rot), links davon eine
Lichtschranke. Mit Preßluft kann der Druck in der "Flasche"
erhöht werden. sektkorken.htm (FB) |
 |
| Abb. 02: Das Ziel: Eine
Papierwand, daneben ein zweites Mikrofon (blau) (FB) |
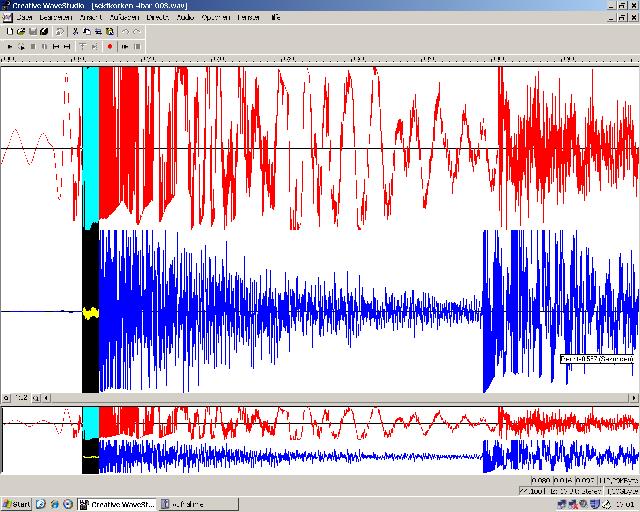 |
| Abb. 03: Die Aufzeichnung der
Geräusche gegen die Zeit: Oben (rot) Mikrofon am Start, unten (blau) Mikrofon am Ziel. Beim Schuß bekommt zunächst das rote Mikrofon ein Signal, nach kurzer Zeit, 0,016 Sekunde (schwarz markiert) ist der Schall beim blauen Mikrofon angekommen. (FB) |
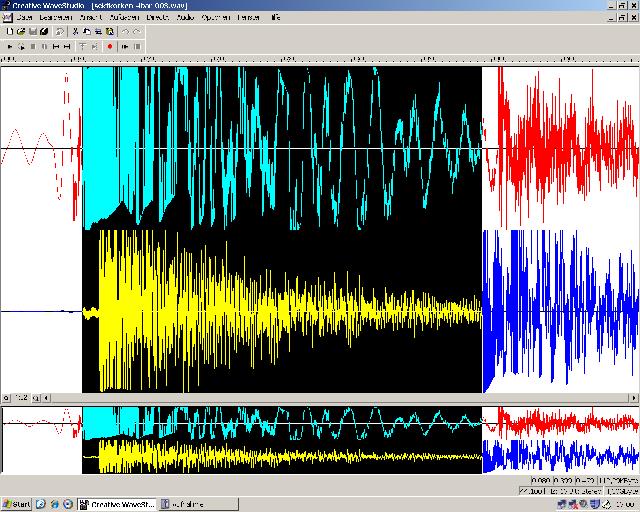 |
| Abb. 04: Nach etwa einer halben
Sekunde, 0,48s (schwarze Markierung) ist der Korken auf die
Papierwand aufgeprallt. Den Knall sieht man am starken Signal des
blauen
Mikrofons. Etwas später erscheint dieses Geräusch auch wieder beim roten Mikrofon.. (FB) |
 |
| Abb. 05: Auswertung der Abb. 04 Rechnung: Laufzeit für den Schall 0,016 s, Flugzeit für den Korken 0,48 s Geschwindigkeit Schall: 5,5 Meter in 0,016 Sekunden ergibt 343 m/s Korken: 5,5 Meter in 0,48 Sekunden ergibt 11,5 m/s (FB) |
 |
| Abb. 06: Berechnung der
Geschwindigkeit bei idealen Bedingungen: keine Reibung beim Start des Korkens im Flaschenhals, keine Luftreibung. Fläche des Korkens 0,0002 m² Druck 3 bar = 300000 N/m² Masse des Korkens 0,0075 kg Bechleunigungsweg 2 cm = 0,02 m für eine gleichförmig beschleunigte Bewegung gilt: s Weg, v Geschwindigkeit, a Beschleunigung, t Zeit Weg s=a/2 t² Endgeschwindigkeit v= a t daraus folgt v = wurzel (2 a s) Ein Rechenfehler hat sich an der Tafel eingeschlichen: Die Kraft ist 300000 mal 0,0002 = 60 (und nicht 150), somit ist die Beschleunigung 60 / 0,0075 = 8000 und die Geschwindigkeit Wurzel (2 mal 8000 mal 0,02) = Wurzel (320) = 16 m/s. (statt 28) das sind etwa 60 km/h (auf der Tafel steht 100 km/h) (FB) |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| Abb. 07a bis ....: Sektkorken im
Flug, Aufzeichnung mit Hochgeschwindigkeitskamera, 462 Bilder pro
Sekunde. Auch hieraus läßt sich die Geschwindigkeit
ermitteln. Etwa 35 cm Bewegung in 10 Bildern ergibt für die Zeit = 10/462 = 21 ms, 0,35 / 0,021 = 16 m/s offensichtlich ist der Korken im Mittel auf den ersten Dezimeter Flugweg noch etwas schneller als bei der 5,5 Meter langen Strecke. |
  Abb. 08a und Abb. 08b: Auf dem Rand des Plattentellers sind für die Einstellung der unterschiedlichen Grund-Geschwindkeiten helle und dunkle Flächen angebracht. Zur Einstellung der richtigen Drehzahl nutzt man eine stroboskopische Beleuchtung mit 50 Hz und dieses periodische Hell-Dunkel-Muster. Bei richtig eingestellter Drehzahl scheint eines dieser Muster zu stehen, trotz Bewegung des Plattentellers. Ist die Drehzahl geringfügig zu hoch, läuft das Muster in Drehrichtung, im anderen Falle entgegen. Diese Art der Geschwindigkeitsmessung arbeitet gut bei einzelnen Objekten. Sie versagt aber bei regelmäßig wiederkehrenden Strukturen, wie hier oder beispielsweise bei der Bewegung einer Ventilatorrades, wenn die einzelnen Flügel nicht unterscheidbar sind. Dann ist die Antwort mehrdeutig. Auch bei der doppelten Drehzahl scheint das Muster zu stehen. (FB) |
 |
| Abb. 09a: Ein zehn Meter langes
Rohr mit zwei Mikrofonen, jeweils am Ende, wird zur Messung der
Schallgeschwindigkeit verwendet. Ein kleiner zerplatzender Luftballon
dient als Schallquelle. Aus der Laufzeit der Echos ergibt sich die
Schallgeschwindigkeit. (FB) |
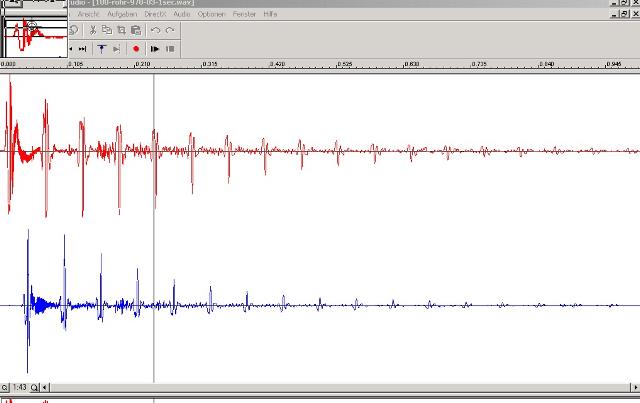 |
| Abb. 09b: Das akustische Signal
an beiden Enden nach dem Zerplatzen des Luftballons ist dargestellt.
Am Mikrofon rot ist der Luftballon zerplatzt. Von Mikrofon rot zum
Mikrofon blau und umgekehrt laufen die Echos. Hier sind es 17 Stück pro Sekunde, d.h. bei 20 Meter Strecke für hin und zurück ergibt sich für die Schallgeschwindigkeit 340 m/s. Tondatei siehe einzel-folge (FB) |
Geschwindigkeitsmessung mit Licht, Lichtgeschwindigkeit, Entfernungsmessung
 |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 10: Modell zur
Geschwindigkeitsmessung mit zwei Lochblenden. Ein Motor dreht die Achse
mit den beiden Scheiben, von oben fallen kleine Stahlkugeln
herab. Fizeau hat mit einem rotierenden Zahnrad die Lichtgeschwindigkeit bestimmt. Er schickte Licht zu einem entfernten Spiegel durch die Zähne eines rotierenden Zahnrades. Wenn das Licht beim Rücklaufen auf die nächste Zahnlücke traf, konnte er aus der Drehzahl und der zurückgelegten Strecke die Lichtgeschwindigkeit bestimmen. (FB) |
Abb. 11: Das kleine Rohr rechts
oben enthält die Stahlkugel. Kommt das offene Segment der Scheibe
am Rohr vorbei, beginnt die Kugel zu fallen. Sind Fallzeit und Umdrehungsgeschwindigkeit aufeinander abgestimmt, trifft die Kugel auf das offene Segment der unteren Scheibe. Aus der Drehzahl und dem Winkelunterschied beider Segmente läßt sich dann die Fallzeit ermitteln. Allerdings ist das Ergebnis nicht eindeutig. Bei doppelter (ganzzahlige Vielfache) Drehzahl gelangt die Kugel auch durch die Öffnung. Bekannter Effekt bei der Darstellung von Speichenrädern im Wildwest-Film. Der Wagen fährt vorwärts, die Räder drehen scheinbar rückwärts. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb.12: Bestimmung der
Lichtgeschwindigkeit nach Foucault.
Ein Lichtstrahl läuft eine Strecke hin und zurück. Auf seinem Weg trifft er auf einen rotierenden Spiegel (beidseitig verspiegelt). Beide Laserstrahlen sind hier in unterschiedlicher Höhe auf dem noch ruhenden Spiegel zu sehen. Drehzahl bis 500 U/s (FB) |
Abb.13: Linse mit dem hin- und
rücklaufendem Laserstrahl (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 14: Hier trifft der
rücklaufende Strahl auf, wenn sich der Spiegel ganz langsam dreht.
(FB) |
Abb. 15: Dreht sich der Spiegel
ganz schnell, dann kommt das Licht einige Millimeter daneben an bei
einem gesamten Laufweg des Lichtes zwischen Drehspiegel und
Reflektorspiegel von etwa 30 Meter. Entfernung vom Drehspiegel bis zur Skala etwa 5 Meter. Drehzahl: 1000 Spiegelflächen pro Sekunde. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 16: Elektrooptischer
Entfernungsmesser Zeiss SM11 , 1971 (FB) |
Abb. 17: Eletrooptisches
Tachymeter, Theodolit mit Entfernungsmesser, Zeiss Elta 2 Die elektronische Bestimmung der Laufzeit war noch etwas aufwendig. (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 18: Reflektorspiegel,
Tripelprisma, wirft das Licht in die gleiche Richtung exakt wieder
zurück. Man sieht das Objektiv der Kamera (FB) |
Abb. 19: Elektrooptischer
Entfernungsmesser. Laserstrahl links und Empfangslinse sind
räumlich getrennt. 2000, DISTO, LEICA (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 20: Elektrooptischer
Entfernungsmesser, Laserentfernungsmesser, montiert auf Drehteller mit
Motor und Winkelmessung JENOPTIK (FB) |
Abb. 21: Laserentfernungsmesser
für die Ausbildung (Leybold-Didactic) (FB) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
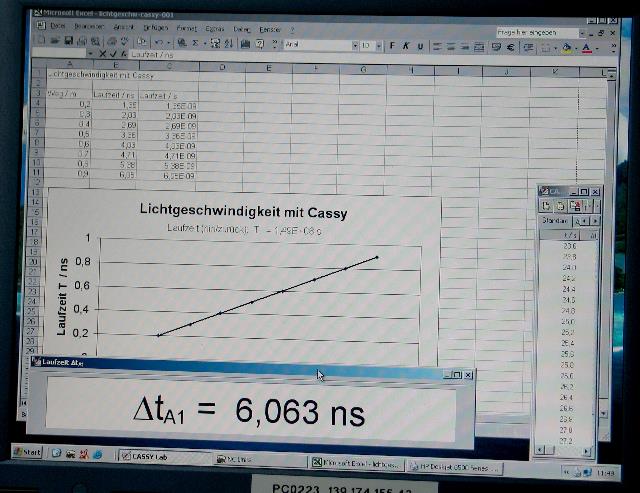
| Abb. 22:
Versuch in der Vorlesung, mit dem Gerät aus der vorherigen
Abbildung wurde eine Strecke gemessen. Die Laufzeit des Lichtes betrug
6 nanoSekunden, d.h. die Strecke ist Lichtgeschwindigkeit mal Zeit, 300 000 000 m/s * 0,000 000 006 = 1,8 m lang Das Licht läuft hin- und zurück, also ist die Entfernung bis zum Ziel 0,9 Meter. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Abb. 23:
Ein Blech mit regelmäßigen Öffnungen und eine
Lichtschranke dienen zur Bestimmung der Fallbeschleunigung. Abstand
einer Sprosse: 4 cm. (FB) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
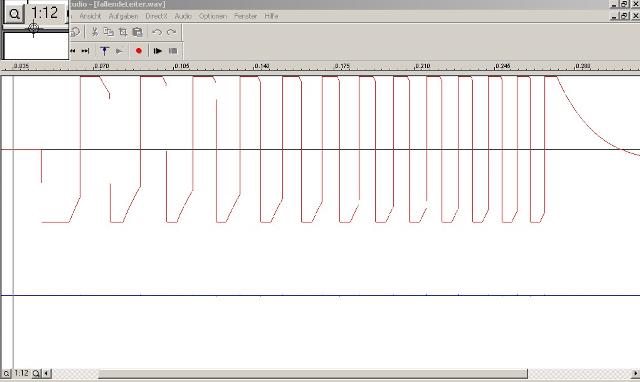
| Abb. 24:
Das Signal an der Lichtschranke, wenn die Leiter fällt. Die
Aufzeichnung hat der akustische Eingang des Rechners, die Soundkarte,
vorgenommen. Das Programm eines Soundkarten-Herstellers erlaubt eine zeitlich aufgelöste Darstellung der Amplitudenwerte, die sich mit dem Mauszeiger abfragen lassen. Für die Auswertung wurden die Zeitpunkte der abfallenden Flanken gewertet. Tondatei (fallendeleiter.wav, Wave-Datei 65 kB) (FB) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tabelle
01: aus den Daten der vorherigen Abbildung wurden für jede Sprosse
beim Durchgang durch die Lichtschranke die Zeiten sowie die
zugehörigen Geschwindigkeit berechnet. Als zugehöriger
Zeitpunkt für die Geschwindigkeit einer Sprosse wurde der
Mittelwert zweier aufeinanderfolgender Zeiten genommen. (FB) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
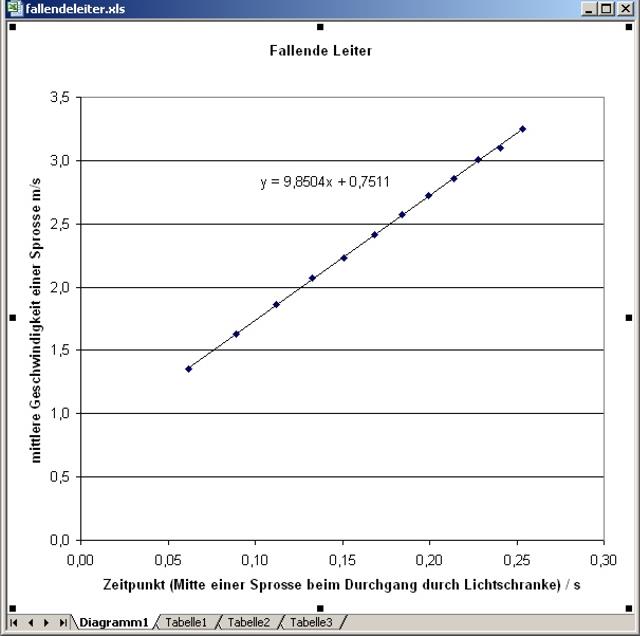
| Abb. 25:
Die Geschwindigkeit der Leiter nimmt proportional mit der Zeit zu. Die Steigung der Kurve entspricht der Beschleunigung der Leiter und hat laut Ausgleichsgeraden den Wert 9,85 m/s² (FB) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nachtrag Februar 2022
2. Verschluss einer Mineralwasser-Flasche
 |
| Abb. 02-00: Flasche auf dem Kopf gehalten, gefüllt mit 25 cm³ Wasser. Das Volumen entspricht etwa dem Gasraum über der Flüssigkeit bei normaler Füllung mit Mineralwasser. (FB) |
 |
| Abb. 02-01: Ein 28 mm T-Stück
(Kupferfitting) hat am linken Ende eine durchbohrte
M5-Messingschraube und am Abgang ein 4 mm dickes Kupferrohr. Das rechte Ende hat mit 28 mm Durchmesser gerade das richtige Maß für einen außen leicht geglätteten Schraubverschluß. Der Verschluß soll von einem Zwirnsfaden gehalten werden. Wenn der Verschluß eingeführt ist, beträgt das verbleibende Volumen rund 25 cm³. (FB) |
 |
| Abb. 02-02: Eine Unterlegscheibe am Ende des
Fadens soll den Verschluß vor dem Abschuß in Position halten. Für die
Durchführung des Fadens wurde der Verschluß in der Mitte durchbohrt. Damit das Geschoß besser abdichtet bzw. gleitet, ist es von außen mit etwas Butter eingeschmiert. (FB) |
 |
| Abb. 02-03: Erster Versuch mit einer Holztür als Ziel. Der gewählte Zwirnsfaden erwies sich als zu schwach. (FB) |
 |
| Abb. 02-04: Das Skalenseil von einem alten Radio
hat bessere Eigenschaften. Die Idee mit dem Durchbrennen des Fadens beim
Abschuß ist bei diesem Material ungeeignet, daher Durchschneiden mit
einer Schere. (FB) |
 |
| Abb. 02-05: Links ist eine Blechtafel, auf die der Verschluß mit hartem Geräusch aufschlagen soll. Zur Tonaufnahme dient das Mikrofon in einem Smartphone. Länge der Flugbahn: 70 cm (FB) |
 |
| Abb. 02-06: Am Ende des dünnen Kupferrohres wird der Druck mit diesem Zeigerinstrument gemessen. (FB) |
 |
| Abb. 02-07: Das Seil läuft nach links über eine
Umlenkrolle und wird von einem Stück Eisenbahnschiene stramm gezogen.
Dahinter steht ein Luft-Kompressor. (FB) |
 |
| Abb. 02-08: Übersicht (FB) |
Versuch 1 |
|||||||||||||||
 |
|||||||||||||||
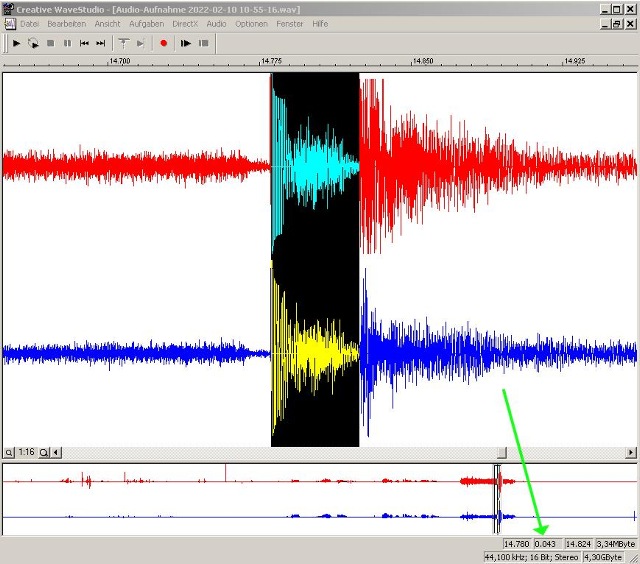
| Abb. 02-09: Analyse der aufgezeichneten Geräusche (Wave-Datei) - Lautstärke gegenüber der Zeit aufgetragen für den rechten und linken Stereo-Kanal. Oberes Fenster: Ausschnitt der Aufzeichnung im unteren Fenster. Der schwarz eingefärbte Bereich beginnt mit dem Knall beim Abschuß und endet mit dem Geräusch beim Aufprall auf die Blechplatte. Beim grünen Pfeil läßt sich die Zeitdifferenz ablesen: 0.043 s. also 43 Millisekunden.
Aus den Daten ergibt sich eine Geschwindigkeit von etwas weniger als 60 km/h |
|||||||||||||||
Versuch 2 |
|||||||||||||||
 |
|||||||||||||||
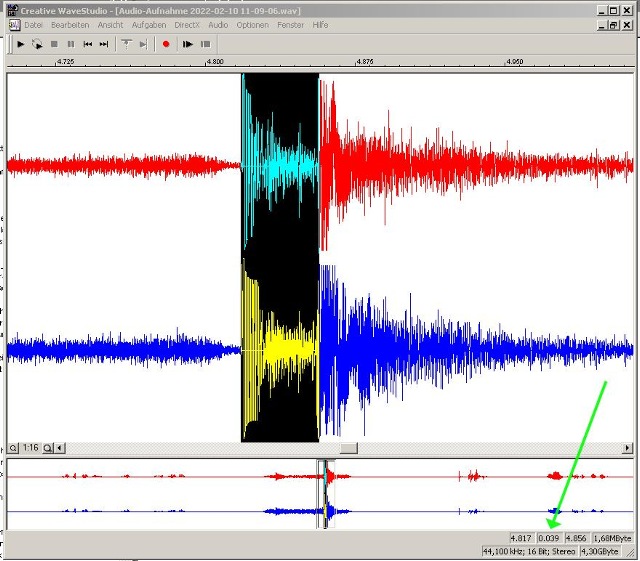
| Abb. 02-10: 39 Millisekunden die Geschwindigkeit ist im Bereich von 65 km/h
|
 |
www.biosensor-physik.de | (c)
28.10.2009 F.Balck 12.02.2022 |
© BioSensor-Physik 2022 · Impressum
